En esta sección se muestran algunos ejemplos típicos de cálculos de momento de inercia por integración. Si bien los problemas se suelen resolver de muchas formas, en la mayoría de los que mostramos aquí intentamos resolver las integrales de la forma más sencilla posible, de forma que no sea necesario la resolución de estos ejemplos mediante integrales dobles o triples.
En primer lugar mostramos en el EJEMPLO 1 un problema de densidad volumétrica, en el EJEMPLO 2, uno de densidad superficial y en EJEMPLO 3 uno de densidad lineal.
Los ejes X, Y y Z de la esfera coinciden con diámetros de la esfera, por tanto, el momento de inercia respecto de estos ejes será el mismo que el calculado en el ejemplo.
Los EJEMPLOS 2 y 3 constituyen también una aplicación del Teorema de los ejes perpendiculares
 |
El EJEMPLO 4 es similar al EJEMPLO 1, pero con una diferencia fundamental, la esfera es hueca, es decir, una corteza esférica sin espesor |
El EJEMPLO 5 es un problema donde aparece el concepto de densidad lineal de masa
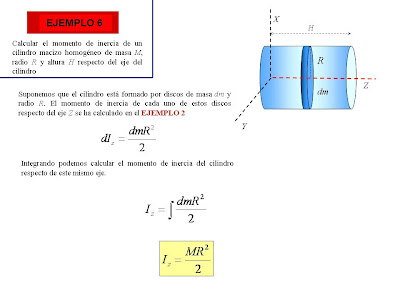
En este EJEMPLO 5 podemos observar que el momento de inercia respecto del eje X de la varilla delgada sería nulo, al estar la varilla situada sobre dicho eje.Muchas veces, como vemos en este EJEMPLO 6, descomponiendo la figura en figuras sencillas, la integración resulta muy sencilla.
Lo mismo ocurre en este EJEMPLO 7.
Para ver la Semejanza de Triángulos se puede consultar la dirección Web: http://mimosa.pntic.mec.es/clobo/geoweb/semej3.htm
El binomio de Newton, se puede calcular con esta otra página Web: http://thales.cica.es/rd/Recursos/rd99/ed99-0516-02/practica/binomio.html

En este EJEMPLO 9 hemos utilizado la conocida expresisón suma de cuadrados por diferencia de cuadrados , http://sipan.inictel.gob.pe/internet/av/producto.htm